Un mērķis šādam eksperimentam ???
Es vēlreiz atļaušos uzsvērt ka meridiāni un paralēles ir SPECIĀLA KONSTRUKCIJA, tāpēc "random" zīmējums uz sfēras nekādi nav savelkams kopā ar ģeogrāfiski un matemātiski pareizu konceptu.
Es neākstos, es tikai nespēju šobrīd izdomāt kā tev to labi paskaidrot.
P.S. celtnieka instruments ir piemērots 2 D plaknei, bet neder nekam 3D telpā, tādēļ ka tā vienīgais pareizas lietošanas priekšnosacījums ir "paralēlisms" konkrētai plaknei ( ar līmeņrādi) kas tavā atrašanās, jeb mērīšanas punktā pieskaras zemei/sfērai. Un šī plakne tikai šķērso kaut kādos noteiktos leņķos mūsu intersējošās meridiānu un paralēļu plaknes ( ja mēs tās paturpinam ārpus sfēras). Un tie leņķi tad gan ir mainīgi atkarībā no mūsu atrašanās vietas uz sfēras, gluži kā tu domā.
Es nezinu varbūt tev no šī izdodas saprast kā "tur tas" 3D 90 grādu leņķis veidojas, :
Bet kospummā es nevaru atrast patreiz tādu labu viegli sagremojamu info par leņķa starp 2 plaknēm mērīšanu.
Te var provēt apskatīt video, bet vairāk noderīgs kā angļu val. atslēgas vārdu "resurss", jo nepalīdz viegli izprast jautājumu par plaknēm kontekstā ar mūsu interesējošo sfēru.
te vēl prasās kā minimums skaidrojums par šo "objektu" :
Tas būs atkarīgs no tā ko tu šajā gadijumā uzskati par 90 grādiem. Ja tu paņemsi celtnieka instrumentu un pagriezīsies pa 90 grādiem, rezultāts būs nosacīta "taisne" kas ies prom no Z-pola, ja tu izmantosi ģeogrāfiski un matemātiski pareizu 90 grādu leņķi attiecībā pret meridiānu - tu riņķosi ap Z-polu. ;)
Tas ir jautājums par pareizu leņķa mērīšanu katram no gadījumiem, un matemātiskā un ģeogrāfiskā leņķa mērīšana ir balstīta uz noteiktu teoriju. Un problēma rodas, ka vienā gadijumā tu mēri 90 grādus "2D plaknē" pa lielam liekot "stūri" kā pagadās, ar domu ka mēģini to likt "paralēli" zemes virsmai, bet otrā gadījumā tu mēri leņķus "pa taisno" 3D telpā, un tie ir faktiski leņķi kas ir starp 2 plaknēm.
Vēl viens veids kā "tauta" šmaucas - ir iespējams nopirkt "autora vietu" kāda cita veiktā pētījumā:
Attiecīgi jautājums vai tas ir veids kā panākt ka autors kļūst "vairāk respektēts" publikāciju skaita dēļ, vai arī publikācijai nepieciešams "zināms" vārds, lai to vispār kāds publicētu ...
Tā jau nav problēma - man mājās ir globuss.
Vienkārši vizuāli tev rodas maldīgs uzskats par leņķi, tā kā uz sfēras virsmas "taisna līnija" vairs vizuāli nav taisna, kaut pēc būtības tā ir riņķa līnija vai tās daļa, kura pieder vienai vienīgai plaknei.
Un tālāk tā kā vēl nav labu ideju varu tikai piedāvāt mācību materiālu par plaknēm un taisnēm ...
ocw.ehu.eus/pluginfile.php/51123/mod_resource/content/2/3teoria_english.pdf
NU ši jau nav būvēts al la LV apstākļiem, bet jebkam kas ir ASV "uz vietas" un kur ASV varētu "iebāzt savu degunu", tomēr dīzēlis ir stipri karstāks pasākums. Es gan teikšu godīgi - nav bijusi daŗišana ar dīzeļu močiem, bet divtaktu dīzeļiem dzesēšana ir diezgan paliela problēma kalnainā apvidū īpaši ASV siltajos štatos, un pat par 30% aizsists radiators var uztaisīt palielas ziepes)
ASV relatīvi vecie busi ir ar 2 taktu dīzeļiem biezā slānī.
Ir savi plusi un savi mīnusi, ja iznāk "vilkties" pa stipri nelīdzenu virsmu - var nepietikt
tehniski korekti būtu virzīt "sfēru sfērā" tikai pa šo "centrālo" Z-D pola asi, vai attiecīgi griezt ap šo asi, bet nu tas nepalīdz izpratnei ...
Idejiski paralēles ir speciāla konstrukcija uz savstarpēji paralēlām plaknēm, un meridiāni dala visu sfēru vienādos sektoros. Kaut droši labāks skaidrojums ir pati meridiāna vai paralēles definīcija ...
Ehh es padomāšu par labāku ilustrāciju, jo problēma ir tajā ka paralēles un meridiāni ir speciāla ģeometriska konstrukcija kura strādā tieši ar vienu rotācijas asi kas iet caur D un Z poliem. Tādēļ mēģināt to grozīt ap citu asi - nav korekti, nu jeb dos pavisam citu rezultātu nekā "paredzēts" !
Es saprotu no kurienes rodas šis secinājums, taču faktiski tu sfēras virsmai uzstiep Eiklīda plakni, bet Eiklīda plakne pēc būtības tikai pieskaras sfērai, pie kam ja tagad smadzene nostrādāja pareizi, tad tikai 1 punktā. Tādēļ 3 dimensiju telpā uz sfēras to nav viegli iztēloties ...
savstarpējais leņķis kā reizi paliek 90 grādi vienalga kuru paralēli ņemsi, tādēļ ka plaknes ir perpendikulāras
P.S. taviem vārdiem - tas ir "pārceltā ekvatora līnija sakrīt ar konkrēto paralēli un veido 90 grādu leņķi ar meridiānu
Ā ok, nu tur jau ir atbilde pašā nosaukumā - tās ir paralēles, tieši tāpēc ka rinķis kas veidojas no ekvatora (kā Eiklīda plakne) ir paralēls jebkuram citam riņķim kurš veido vienu plakni ar konkrēto vai jebkuru paralēli.
"Kretīnismu" ievieš tikai kompasa lietošana, un tad vēl arī atkarībā no atrašanās vietas.
Sorry es apzinos ka manas paskaidrošanas spējas šobrīd iespējams ir dziļā pakaļā ...
p.S. taviem vārdiem - tas ir "pārceltā ekvatora līnija sakrīt ar konkrēto paralēli un veido 90 grādu leņķi.
Ehh un arī te - Grinviča ir laža - latviski pareizi ir Griniča( Greenwich)
galva vairs nestrādā - sorry
Un tehniski tas nozīmē apmēram 0-4 grādu atšķirību starp ģeogrāfisko (meridiāni un paralēles) un kompasa rādījumu, atkarībā no tā cik tuvu/tālu atrodies jebkuram no 2 meridiāniem kuri atrodas vienā plaknē (Eiklīda) ar magnētisko Z -polu.
Bet citādi ņemot vērā šos "kompasa melus" tie ir tieši tie 90 grādi.
P.S. par meridiāniem gan es šķiet varētu būt "pārliecis", tā kā tiem ir sakars ar Grinviču, nevis magnētisku polu, t.i. teikšu godīgi nezinu vai kāds meridiāns vispār ir pat tuvu magnētiskam Z-polam, es te vairāk par konceptu "uz sfēras" .
Nesapratu jautājumu līdz galam !
Te ir kā tas izskatas "no sāna" no kura var pamanīt "vislielāko" nobīdi :
teara.govt.nz/en/diagram/9213/earths-magnetic-field
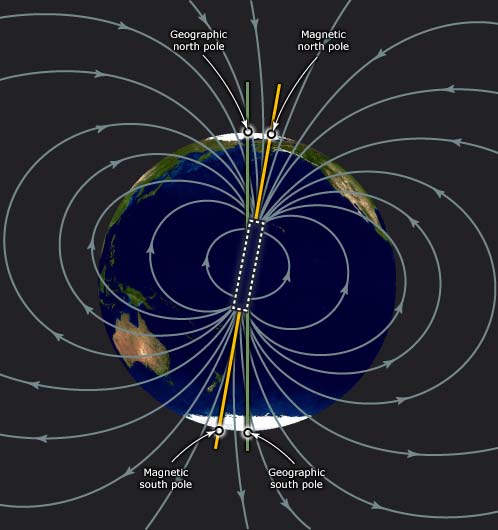
Es gribu teikt ka kompasa 90 ir tieši TIE 90 (lai arī ir mikroskopiska - reizēm līdz pat 800 jūdzēm "liela" nianse dēļ magnētiskā pola faktiskās atrašanās) starp meridiānu un paralēlēm.
Nu bet paskaties to pašu kvadrātu ar 120 grādu leņķiem uz sfēras virsmas - varbūt tad būs vieglāk saprast ...
Liels retums - dīzeļa motocikls ASV armijai:
Kāpēc ne vienmēr "veicas" ar plastmasu otrreizēju izmantošanu :
FYI:
en.wikipedia.org/wiki/Meridian_(geography)
... each meridian is perpendicular to all circles of latitude.
To nav grūti aptvert, ja skatās uz jebkuru vienu individuālu meridiānu !
Sfēras virsmas "paradokss" ir ka "trīsstūris" var būt ar trim taisniem leņķiem, un ka "kvadrāts" uz sfēras virsmas saturēs četrus 120 grādu leņķus ...
LC Prado, ja nu kas (jeb tas kurš LC 90 pēctecis, tātad LC120, LC 150 ...).
Prada ir modes nams - ja nu kas ! ;)
Tas ir rezultāts "zonas beigām", lai arī šāds krāvums varbūt ir pirmoreiz, taču "salidojumi" ir bieži redzēti ...
Portālā publicētie autoru viedokļi var atšķirties no iAuto redakcijas viedokļa.
Pareizi - lai būtu viegli izrēķināt atrašānās vietu - bet tā ir speciāla konstrukicja tieši šim nolūkam, kur visu paralēļu viedoto plakņu normāle ( vektors kurš ir perpendikulārs visām taisnēm kas pieder konkrētai plaknei) sakrīt ar nosacīto zemes asi kas savieno D un Z polus.
Un savukārt meridiānus "saturošās" plaknes - riņķi visi iet caur/ satur šo normāli, attiecīgi uzzīmējot jebkuram merdiāna riņķim plaknei normāli - tā vienmēr būs perpendikulāra ar Z-D pola asi ... tādēļ tās vienmēr ir perpendikulāras plaknes.
----
Uzzīmējot + uz sfēras jebkurā vietā tu neko nepasaki par plaknēm, un 3D telpu - tu rupji sakot atzīmēji vienu punktu uz virsmas un viss.